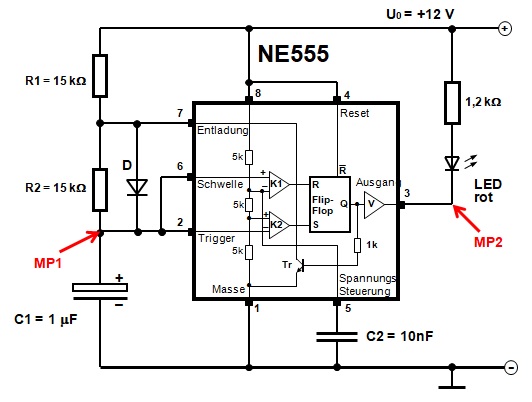
Mit wenigen Bauelementen kann das Timer-IC NE555 zum astabilen Multivibrator geschaltet werden.
Den Schaltplan für den Multivibrator zeigt das nächste Bild.

Mit den Widerständen R1 und R2, dem Kondensator C1 und der Diode D erhält man eine gleiche Auflade-
und Entladezeit am Kondensator C1, wenn R1 und R2 gleichgroß sind.
An den Messpunkten MP1 und MP2 werden die periodischen Spannungsverläufe mit Hilfe eines digitalen
Speicheroszillografen, Fabrikat RIGOL DS1052E, dargestellt.
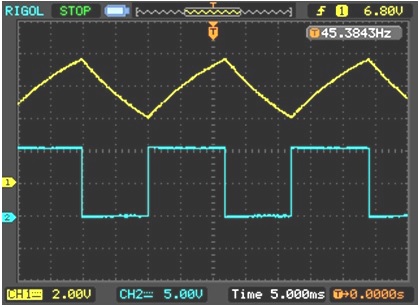
Die Aufladung an C1 beginnt bei 1/3 der Spannung Uo und endet, wenn 2/3 von Uo erreicht werden. Dann
beginnt die Entladung von C1 bis auf 1/3 von Uo.
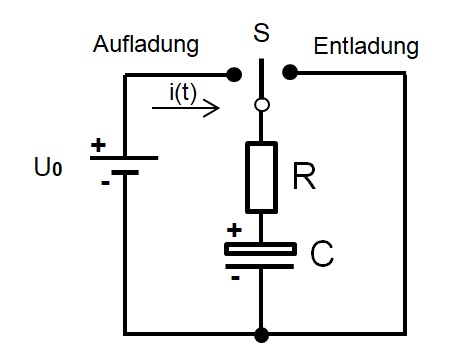
Anhand einer einfachen Schaltung werden nun die zeitlich veränderlichen Größen, wie Strom i(t) und
Spannung u(t) am Kondensator berechnet.
Bei einer zeitlichen Änderung der Kondensatorspannung fließt der Strom:
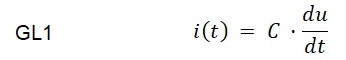
Befindet sich der Kippschalter S in der Stellung Aufladung, zeigt Gleichung GL2 die Spannungsaufteilung.
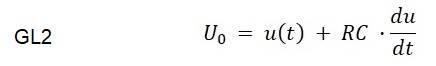
Nach Umformung erhält man Gleichung GL3:
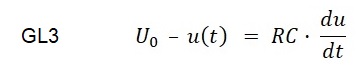
Nach einer weiteren Umformung erhält man Gleichung GL4 mit der Trennung der Veränderlichen:
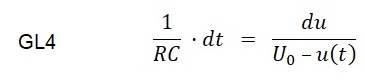
Die Integration der linken Seite von GL4 bereitet keine Schwierigkeiten.
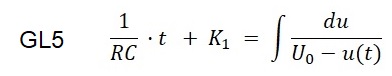
Die rechte Seite ist ein unbestimmtes Integral, deren Lösung aus meinem "Taschenbuch der Mathematk"
von Bronstein-Semendiajew 1964, Seite 297 stammt:
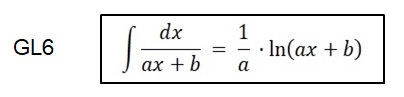
Mit a = -1, b = Uo und dem Ersetzen dx durch du folgt Gleichung GL7:
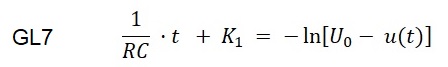
GL7 wird mit multipliziert mit -1 und man erhält:
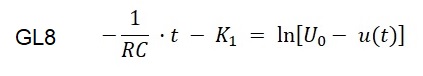
Nun erfolgt der Übergang auf die Exponentialschreibweise:
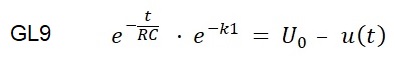
Aufgelöst nach u(t) folgt:
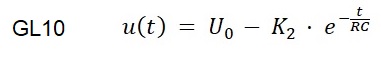
Mit den Anfangsbedingungen bei t = 0 ist u(0) = 0 lautet die Bestimmungsgleichung für K2
0 = Uo - K2, d.h. K2 = Uo.
Jetzt endlich erhalten wir die mathematische Formel für den Aufladevorgang am Kondensator:
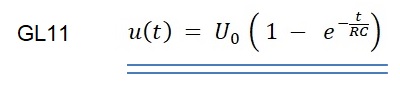
Mit der Programmiersprache GNUPLOT lassen sich mathematische Formeln in Grafiken umwandeln
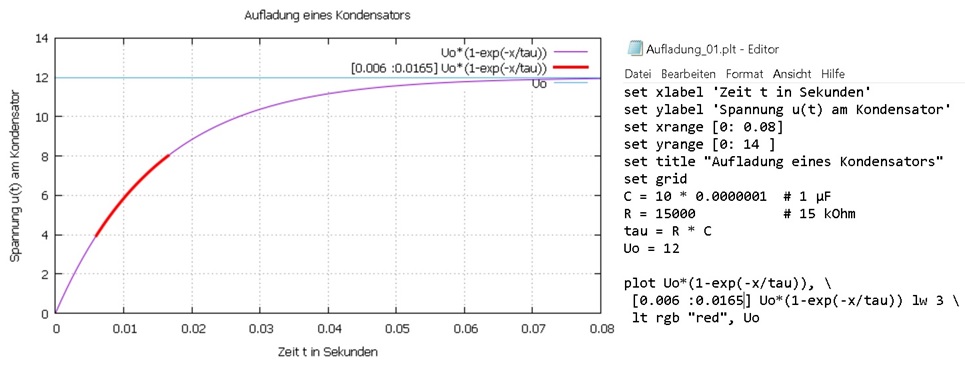
Die Aufladekurve steigt am Anfang fast linear an und nähert sich dann langsam dem Endwert Uo.
In der Aufladekurve ist der Zeitbereich von 1/3 Uo bis 2/3 Uo rot eingefärbt. Dieser gebogene
Kurvenzug ist dem Verlauf im oben gezeigten Oszillogramm sehr ähnlich.
Das Produkt R · C hat die Dimension einer Zeit und wird daher Zeitkonstante
t genannt. Mit R = U/I
und C = Q/U, wobei Q = I · t ist, folgt U/I · I ·
t/U = t.
Ein einfaches Schaltbild für die Entladung des Kondensators C zeigt das nächste Bild:

Nach dem Schließen des Schalters S beginnt die Entladung. Für die Kondensatorspannung und dem
Spannungsabfall am Widerstend R gilt der folgende Zusammenhang:.
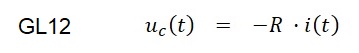
Die zeitliche Spannungsänderung am Kondensator hat den Strom i(t) zur Folge:
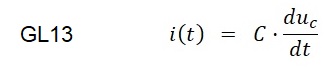
Gleichung GL13 wird in Gleichung GL12 eingesetzt und man erhält:
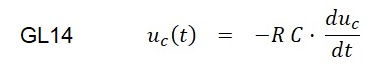
Nach Umformung erfolgt die Integralbildung in der Form:
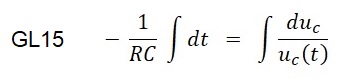
Die Lösung lautet:
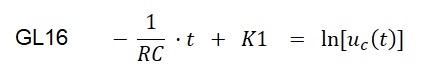
In Exponentialschreibweise erhält man:
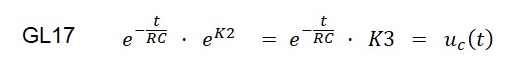
Mit der Anfangsbedingung zum Zeitpunkt t = 0 ist uc(t) = Uo lautet die Lösung für K3:
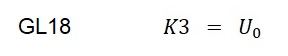
Damit folgt die Zeitkunktion für die Entladung:
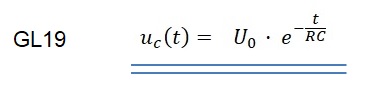
Mit der Programmiersprache GNUPLOT erfogt die Umwandlung der mathematischen Formel in eine Grafik:
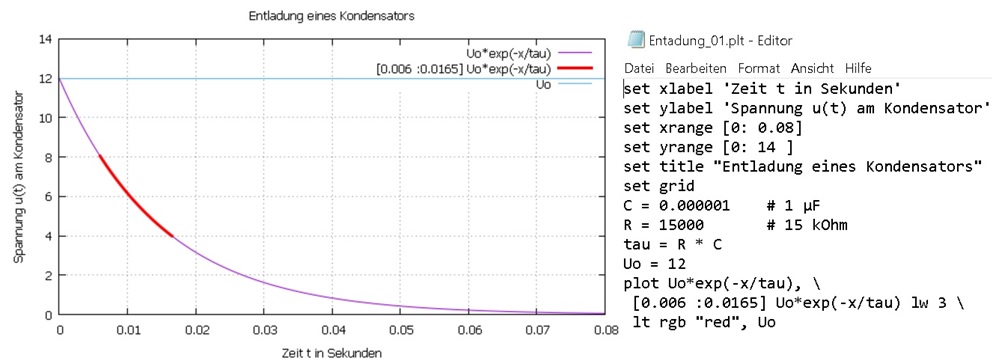
Die Entladekurve fällt am Anfang fast linear ab und nähert sich dann langsam dem Nullwert.
Den berechneten Kurvenabschnitt für die Aufladung und den Kurvenabschnitt für die Entladung werden
nebeneinander angeordnet und ergeben eine Sägezahnkurve.
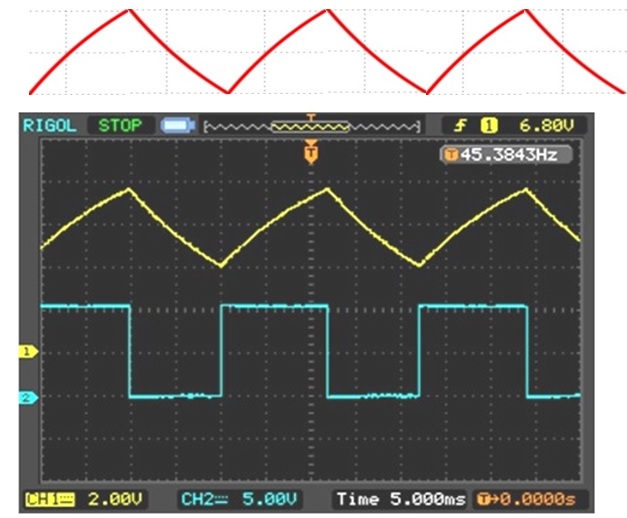
Der Vergleich mit dem Oszillogramm zeigt eine gute Übereinstimmung.
Zurück zur Homepage