Vor mehr als zehn Jahren haben Ute und ich eine Ägypten-Rundreise gebucht mit einer Nil-Kreuzfahrt von
Luxor nach Assuan, einer Busfahrt zum Tempel Abu Simbel. Dann ging es zurück auf dem Nil bis nach Luxor
mit der Tempelanlage von Karnak und dem Tal der Könige. Danach flogen wir nach Kairo und besichtigten
das Ägyptische Museum, die Mohammed-Ali-Moschee und die drei Pyramiden bei Gizeh. Es war für uns ein
beeindruckendes Erlebnis, ganz dicht am Rand der riesigen Pyramiden entlang zu gehen.
Der Anblick der Chephren-Pyramide, rechtes Bild, bleibt für mich unvergesslich. Nach unserer Rückkehr nach
Weinheim habe ich einige Wochen später zur Erinnerung an die Pyramiden ein Modell der Chephren-Pyramide
nachgebaut. Dieses Modell mit indirekter Beleuchtung zeigt das folgende Bild:
Von meinen sechs Enkelkindern ist Bennet der Älteste und wird in diesem Jahr 12 Jahre. Er geht im Nachbarort
in Hemsbach auf das Gymnasium. Vor einigen Wochen besuchte uns Bennet mit seinem Bruder Mats.
Ich war erstaunt, als Bennet von seiner Schule berichtete, dass er schon den Satz des Pythagos aufsagen
kann. Der mathematische Ausdruck lautet: a2 + b2 = c2 . In Worten: In einem
rechtwinkligen Dreieck ist die
Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates.
Auch über Pyramiden haben wir uns unterhalten. Kurzerhand zeigte ich beiden Jungs meine beleuchtete Pyramide,
die ich im Gästezimmer aufgebaut hatte. Es ist eine Pyramide mit quadratischer Grundfläche. Ich fragte Bennet,
ob er sich zutraut, die Höhe der Pyramide mit Hilfe des Satzes des Pythagoras zu berechnen, wenn neben der
Grundseite auch die Länge der Mittel-Linie vorgegeben wird. Also Bennet will sich das mal in den nächsten
Tagen überlegen.
Aus eigener Erfahrung kann ich sagen, dass es nicht ganz einfach für einen 12-jährigen Jungen ist, bei einer
derartigen praktischen Aufgabenstellung den Satz des Pythagoras anwenden zu können.
Man muss in folgender Reihenfolge vorgehen: Mit einer skizzenhaften Zeichnung von der Pyramide ist in der
Pyramide ein rechtwinkliges Dreieck einzuzeichnen, das mit der Höhe h, die Seitenlinie s und mit der Hälfte der
Grundseite a/2 beschriftet wird.
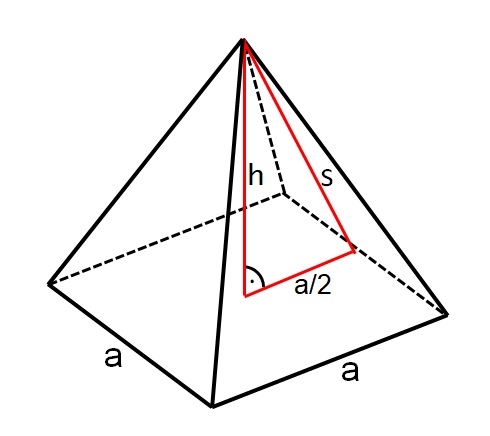
Für dieses rote rechtwinkelige Dreieck gilt: h2 + (a/2)2 = s2 .
Die Lösung für h2 lautet:
h2 = s2 - (a/2)2 .
Mit a = 40 cm und s = 34,5 cm ist h2 = 790 . Mit Hilfe eines Schultaschenrechners, z.B. der Taschenrechner
von Texas Instruments TI-30 ECO RS, kann die Wurzel von h2 gezogen werden.
Das Ergebnis lautet: Die Höhe der Modellpyramide beträgt h = 28 cm .
An einem rechtwinkligen Dreieck mit den Eckpunkten A, B, und C und den Seitenlinien a, b, und c
werden die quadratischen Flächen a2, b2 und c2 gezeichnet.
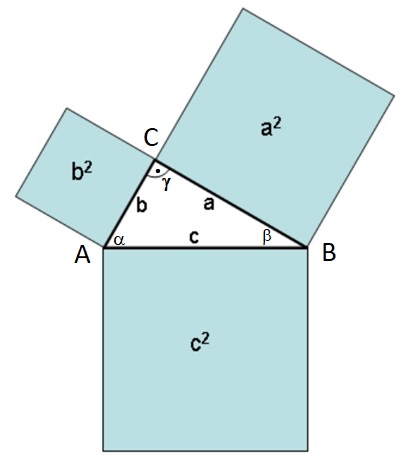
Die dem rechten Winkel gegenüberliegende Seite c ist die Hypotenuse. Aus dem Griechischen (ypo) = unten
und (teinein) = sich erstrecken. Die anderen beiden Seiten a und b, die den rechten Winkel bilden, heißen
Katheten. Aus dem Griechischen: (kathienai) = herablassen.
Der Satz des Pythagoras lautet nun: Der Flächeninhalt des Hypotenusenquadrates ist gleich der Summe der
Flächeninhalte der Kathetenquadrate.
Am Ende des Besuches von Bennet und Mats wurde ich von den beiden gefragt, ob ich eine Grabkammer in
die Modellpyramide einbauen könnte. Nachfolgend berichte ich über dieses nicht ganz einfache Vorhaben.
Eine zu besichtigende Grabkammer in der Pyramide erfordert eine Öffnung in einer der Seitenflächen.
Ich habe mich entschlossen mit einer Laubsäge eine 8 x 12 cm Klappe auszusägen. Ein Scharnier ermöglicht
das Öffnen und Schließen der Klappe.
An der Innenseite der Klappe müßte es möglich sein, mit Hilfe einer dünnen Gewindestange und einem
Schneckengetriebe motorisch das Öffnen und wieder Schließen der Klappe zu realisieren.
Ein brauchbares Schneckengetriebe mit Motor stammt aus den Beständen unseres Modelleisenbahnclubs,
es ist ein motorisch angetriebener Weichenantrieb für eine Unterflurmontage:
Das Schneckengetriebe kann die kleine Gewindestange mit einem Durchmesser von 3 mm
nach rechts und nach links bewegen.
Den Schaltplan zur Drehrichtungsumkehr des Motors zeigt das folgende Bild:
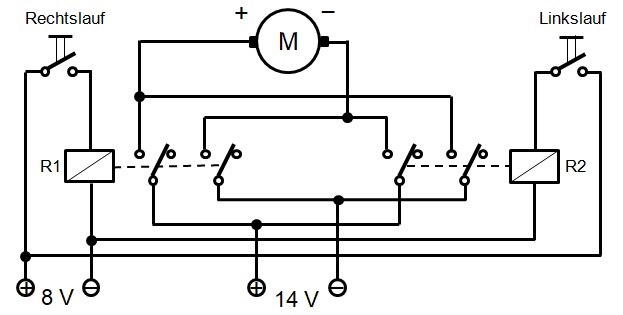
Der Motor mit Gewindestange befindet sich im Inneren der Pyramide. Mit halb geöffneter Klappe
wird diese Anordnung nachfolgend gezeigt:
Neben der Pyramide befindet sich das kleine Steuerpult mit den zwei Drucktastern zum Öffnen
und Schließen der Pyramiden-Klappe:
Die Wände der Grabkammer sind mit ägyptischen Motiven aus Pharaonengräbern ausgekleidet.
Der geöffnete Sarkophag ist mit Goldfolie ausgekleidet.
Für meine sechs Enkelkinder habe ich noch eine Nahaufnahme von der kleinen Grabkammer
angefertigt:
Mit meinem Camcorder, SONY HDR-CX240E, habe ich den Versuch unternommen, den Ablauf des Öffnens
und des Schließens der Grabkammer zu filmen. Auf dem Tonkanal hört man Gebetsrufe im Islam.
Klicken Sie einfach auf den
Pyramiden-Film.
Im Internet findet man bei Wikipedia den
geometrischen Beweis für den Satz des Pythagoras.
Die Beweisführung erfolgt anhand der folgenden Abbildung:
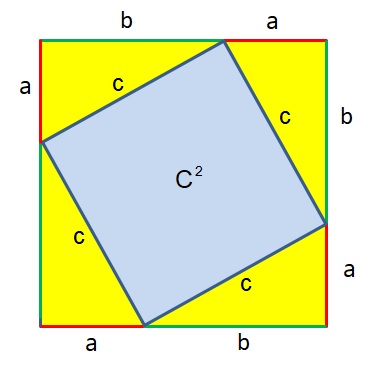
1. Ein großes Quadrat mit der Seitenlänge a + b wird gezeichnet.
2. Die Seitenlinien für c werden gezeichnet.
3. Die vier gelben rechtwinkligen Dreiecke haben je eine Fläche a·b/2
4. Die Gesamtfläche der vier Dreiecke beträgt 2a·b .
5. Aus der Abbildung geht hervor: (a + b)2 = c2 + 2a·b
6. Die Ausrechnung ergibt a2 + 2a·b + b2 = c2 + 2a·b
7. Auf beiden Seiten der Gleichung wird 2a·b subtrahiert.
8. Das Ergebnis ist dann a2 + b2 = c2, was zu beweisen war.
Zu Beginn werden zwei zueinander rechtwinkelige Strecken der Länge 1 gezeichnet. Die Verbindungs-
linie der freien Enden ist die Hypotenuse mit der Länge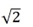 
Den Zahlenwert von 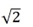können Sie sich leicht merken: Denken Sie an 14 und 14, der
Zahlenwert ist 1,414 .
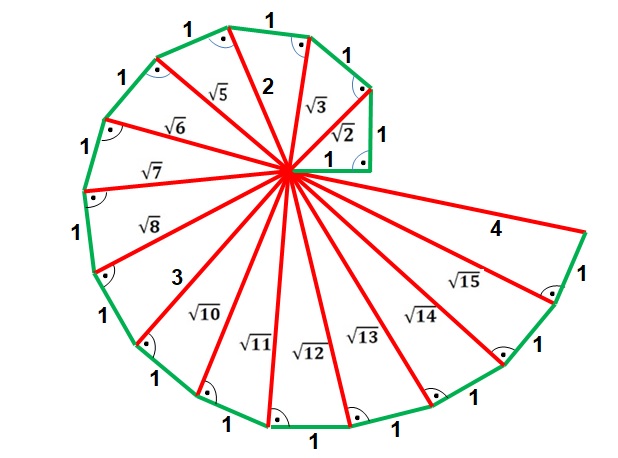
Rechtwinkelig zur Hypotenuse zeichnet man wieder eine Kathete der Länge 1 usw.
Zurück zur Homepage